Unión de Conjuntos
Sean  y
y  dos conjuntos. Se define la unión de
dos conjuntos. Se define la unión de  con
con  , denotada por
, denotada por  (que se lee A unión B), por el conjunto
(que se lee A unión B), por el conjunto

En términos prácticos, la unión de dos conjuntos es el conjunto formado por los elementos de ambos conjuntos.
Sean  y
y  dos conjuntos. Se define la unión de
dos conjuntos. Se define la unión de  con
con  , denotada por
, denotada por  (que se lee A unión B), por el conjunto
(que se lee A unión B), por el conjunto
 y
y  dos conjuntos. Se define la unión de
dos conjuntos. Se define la unión de  con
con  , denotada por
, denotada por  (que se lee A unión B), por el conjunto
(que se lee A unión B), por el conjunto
En términos prácticos, la unión de dos conjuntos es el conjunto formado por los elementos de ambos conjuntos.
Ejemplo
Si tenemos los conjuntos  y
y  , la unión de ellos es el conjunto
, la unión de ellos es el conjunto

Si tenemos los conjuntos  y
y  , la unión de ellos es el conjunto
, la unión de ellos es el conjunto
 y
y  , la unión de ellos es el conjunto
, la unión de ellos es el conjunto
Propiedades de la unión de conjuntos
La unión de conjuntos cumple las siguientes propiedades


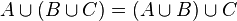

- Si
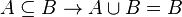
La unión de conjuntos cumple las siguientes propiedades


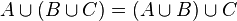

- Si
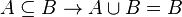
Intersección de Conjuntos
Sean  y
y  dos conjuntos. Se define la intersección de
dos conjuntos. Se define la intersección de  y
y  , denotada por
, denotada por  (que se lee A intersección B), por el conjunto
(que se lee A intersección B), por el conjunto

En términos prácticos, la intersección de dos conjuntos es el conjunto formado por los elementos comunes a ambos conjuntos.
Sean  y
y  dos conjuntos. Se define la intersección de
dos conjuntos. Se define la intersección de  y
y  , denotada por
, denotada por  (que se lee A intersección B), por el conjunto
(que se lee A intersección B), por el conjunto
 y
y  dos conjuntos. Se define la intersección de
dos conjuntos. Se define la intersección de  y
y  , denotada por
, denotada por  (que se lee A intersección B), por el conjunto
(que se lee A intersección B), por el conjunto
En términos prácticos, la intersección de dos conjuntos es el conjunto formado por los elementos comunes a ambos conjuntos.
Ejemplo
Si tenemos los conjuntos  y
y 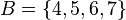 , el conjunto intersección es
, el conjunto intersección es

Nota: Dos pares de conjuntos  y
y  se llaman disjuntos siempre que
se llaman disjuntos siempre que  .
.
Si tenemos los conjuntos  y
y 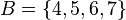 , el conjunto intersección es
, el conjunto intersección es
 y
y 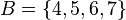 , el conjunto intersección es
, el conjunto intersección es
Nota: Dos pares de conjuntos  y
y  se llaman disjuntos siempre que
se llaman disjuntos siempre que  .
.
 y
y  se llaman disjuntos siempre que
se llaman disjuntos siempre que  .
.Propiedades de la intersección de conjuntos
La intersección de conjuntos cumple con las siguientes propiedades

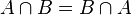


- Si

La intersección de conjuntos cumple con las siguientes propiedades

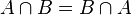


- Si

Diferencia de Conjuntos
Sean  y
y  dos conjuntos. Se define la diferencia de
dos conjuntos. Se define la diferencia de  con
con  , denotada por
, denotada por  (que se lee A menos B), por el conjunto
(que se lee A menos B), por el conjunto

En términos prácticos, la diferencia de un conjunto  con un conjunto
con un conjunto  , en ese orden, es el conjunto formado por todos los elementos que están en
, en ese orden, es el conjunto formado por todos los elementos que están en  pero no están en
pero no están en  .
.
Sean  y
y  dos conjuntos. Se define la diferencia de
dos conjuntos. Se define la diferencia de  con
con  , denotada por
, denotada por  (que se lee A menos B), por el conjunto
(que se lee A menos B), por el conjunto
 y
y  dos conjuntos. Se define la diferencia de
dos conjuntos. Se define la diferencia de  con
con  , denotada por
, denotada por  (que se lee A menos B), por el conjunto
(que se lee A menos B), por el conjunto
En términos prácticos, la diferencia de un conjunto  con un conjunto
con un conjunto  , en ese orden, es el conjunto formado por todos los elementos que están en
, en ese orden, es el conjunto formado por todos los elementos que están en  pero no están en
pero no están en  .
.
 con un conjunto
con un conjunto  , en ese orden, es el conjunto formado por todos los elementos que están en
, en ese orden, es el conjunto formado por todos los elementos que están en  pero no están en
pero no están en  .
.Ejemplo
Si tenemos los conjuntos 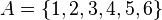 y
y  , entonces el conjunto diferencia de
, entonces el conjunto diferencia de  con
con  es
es

Si tenemos los conjuntos 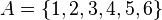 y
y  , entonces el conjunto diferencia de
, entonces el conjunto diferencia de  con
con  es
es
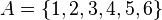 y
y  , entonces el conjunto diferencia de
, entonces el conjunto diferencia de  con
con  es
es
Complemento de un Conjunto
Sea  un conjunto dentro de un conjunto universo
un conjunto dentro de un conjunto universo  . Se define el complemento de
. Se define el complemento de  , denotado por
, denotado por 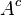 (que se lee A complemento), al conjunto
(que se lee A complemento), al conjunto

En términos prácticos, el complemento de un conjunto es todo lo que no está en el conjunto.
Sea  un conjunto dentro de un conjunto universo
un conjunto dentro de un conjunto universo  . Se define el complemento de
. Se define el complemento de  , denotado por
, denotado por 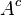 (que se lee A complemento), al conjunto
(que se lee A complemento), al conjunto
 un conjunto dentro de un conjunto universo
un conjunto dentro de un conjunto universo  . Se define el complemento de
. Se define el complemento de  , denotado por
, denotado por 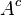 (que se lee A complemento), al conjunto
(que se lee A complemento), al conjunto
En términos prácticos, el complemento de un conjunto es todo lo que no está en el conjunto.
Ejemplo
Si tenemos los conjuntos  y
y  , entonces el complemento de
, entonces el complemento de  es el conjunto
es el conjunto

Si tenemos los conjuntos  y
y  , entonces el complemento de
, entonces el complemento de  es el conjunto
es el conjunto
 y
y  , entonces el complemento de
, entonces el complemento de  es el conjunto
es el conjunto
Propiedades del complemento de un conjunto
El complemento de un conjunto cumple las siguientes propiedades

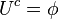


El complemento de un conjunto cumple las siguientes propiedades
Propiedades Combinadas
Se cumplen las siguientes propiedades entre conjuntos



Leyes de distribución
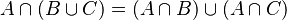

Leyes de De Morgan


Conjunto Potencia
En matemáticas, el conjunto potencia de un conjunto dado es otro conjunto formado por todos los subconjuntos del mismo. Por ejemplo, el conjunto potencia de A = {1, 2, 3}es:

El conjunto potencia de A también se denomina conjunto de las partes de A, o conjunto de partes de A se denota por P(A) o 2A.
Se cumplen las siguientes propiedades entre conjuntos
Leyes de distribución
Leyes de De Morgan
Conjunto Potencia
En matemáticas, el conjunto potencia de un conjunto dado es otro conjunto formado por todos los subconjuntos del mismo. Por ejemplo, el conjunto potencia de A = {1, 2, 3}es:
El conjunto potencia de A también se denomina conjunto de las partes de A, o conjunto de partes de A se denota por P(A) o 2A.
No hay comentarios.:
Publicar un comentario