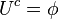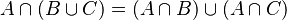Problemas
En un grupo de 100 persona se encuentra que hay 95 aficionados al futbol, 75 aficionados a las carreras de fórmula 1, 80 aficionados al balonmano y 85 aficionados al ciclismo. Calcular el número mínimo de personas aficionadas a los cuatro deportes..
El problema se puede resolver como sigue: Tomamos la nomenclatura: F = 95 ; A = 75 ; B = 80 ; C = 85 y consideramos los conjuntos F, B y C.
Veamos el número de personas aficionadas a los tres deportes, aplicando la relación entre las medidas de los conjuntos, es decir, entre sus cardinales:
Veamos el número de personas aficionadas a los tres deportes, aplicando la relación entre las medidas de los conjuntos, es decir, entre sus cardinales:

 y
y  dos conjuntos. Se define la unión de
dos conjuntos. Se define la unión de  (que se lee A unión B), por el conjunto
(que se lee A unión B), por el conjunto
 y
y  , la unión de ellos es el conjunto
, la unión de ellos es el conjunto


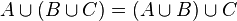

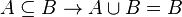
 (que se lee A intersección B), por el conjunto
(que se lee A intersección B), por el conjunto
 y
y 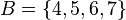 , el conjunto intersección es
, el conjunto intersección es
 .
.
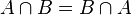



 (que se lee A menos B), por el conjunto
(que se lee A menos B), por el conjunto
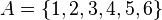 y
y  , entonces el conjunto diferencia de
, entonces el conjunto diferencia de 
 . Se define el complemento de
. Se define el complemento de 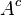 (que se lee A complemento), al conjunto
(que se lee A complemento), al conjunto
 y
y  , entonces el complemento de
, entonces el complemento de